Summary
This project was part of the course Numerical Analysis at KTH. The task was to solve the Kepler problem approximately over long time using different numerical methods. Then we compared the difference between the different methods.
The main purpose was to study Hamiltonian systems and thereby we needed to prove that the Kepler Equations is a Hamiltonian system. We used forward Euler, backward Euler, symplectic Euler, midpoint method and ode45 as different numerical ways to solve the Kepler problem.
The project was further continued with pure mathematical parts where we numrically solved other Hamiltonian systems as the Wave Equation (using d'Alemberts formula) and the Schrodinger Equation as well as investigated the Verlets method. The main conclusion of the project was that it is an advantage to use symplectic Euler when solving Hamiltonian systems in a numerical way since this approach conserves the energy in the best way of the different methods.
Technical Walkthrough
The Kepler Problem looks like following:

For a Hamiltonian system the following equation is satisfied and further we proved that the energy is constant for any Hamiltonian system (for the exact solution).
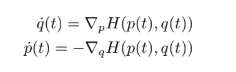
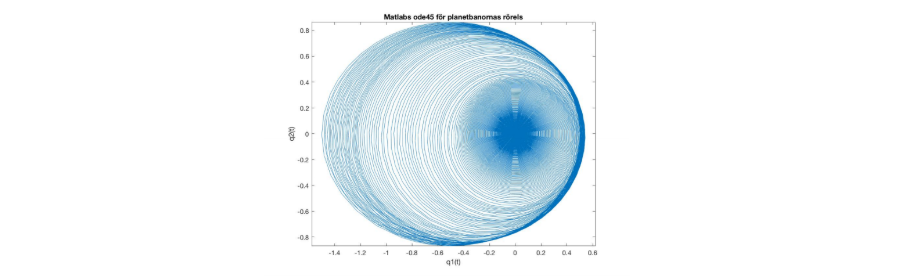
To being able to compare the different numerical methods we plotted the trajectories in a 2D coordinate system. Since the Kepler problem equations describe the so called "two body problem" where two bodies attracts eachother. Newton prooved mathematically that the trajectory turns out to be an elliptical shape with an excentricity a that is between 0 and 1.
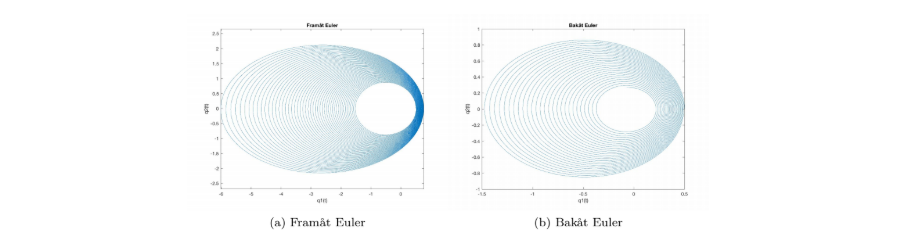
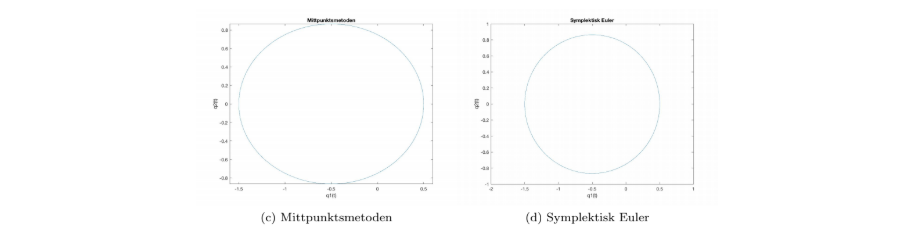
Below you can find the trajectories for the forward Euler, backward Euler, midpoint-method and symplectic Euler.
We continued on with plotting the energy as function of time for the different methods:
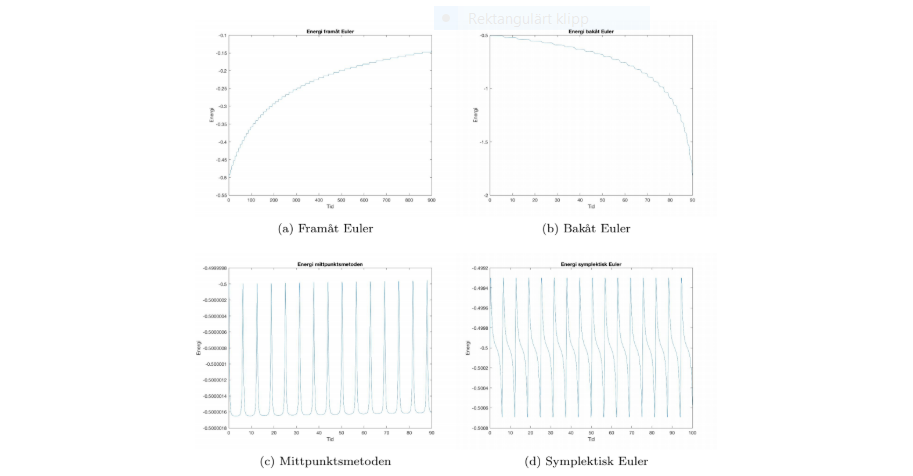
We could see that the different methods have different energy preservance. In the forward Euler, the energy goes up with time and the opposite for the backward Euler (which means that the planet trajectory goes inwards towards the center of the ellips).
For the other two methods (midpoint and symplectic) the energy is almost constant over time and we can see this in the trajectories since they are moving in the same trajectory (not going inwards or outwards). Since we know that planets move in constant trajectories we conclude that the two last methods are the best to use for numerical solution in the Kepler case.
We did the same analysis for the ode45 in Matlab and we could see that the trajectory quickly falled into the middle and thereby concluded that this is not a preferable method for simulating trajectories.